Mechanik-Skripte
In diesem Bereich finden Sie Online-Skripten die das Gebiet der Balken-Biegung umfassen.
Die Berechnung der Biegung von Balken ist ein wichtiges Teilgebiet der Technischen Mechanik und Festigkeitslehre. Hier lernen Sie die Grundlagen der Biegetheorie und lernen die Biegung eines Balkens zu berechnen.
Für die Ermittlung von Größen wie der Durchbiegung, Biegewinkel oder Biegelinie existieren unterschiedliche Biegetheorien. Hier werden zum Beispiel bestimmte Annahmen für die Eigenschaften des Balkens getroffen werden, mit dem Ziel die Berechnung zu vereinfachen und dabei, innerhalb definierter Rahmenbedinungen, immer noch brauchbare Ergebnissen zu erhalten.
Die Biegung ist eine Belastungsart, die in der technischen Mechanik besonders stark durchleuchtet wird, da sie besonders häufig auftritt. Betrachtet werden dabei schlanke Bauteile (Balken oder Bögen) oder dünne Bauteile (Schalen oder Platten).
Die Bezeichnung Biegung bzw. Biegebelastung ist dabei selbsterklärend. Es werden jedoch verschiedene Arten der Biegung unterschieden, die im Folgenden näher erläutert werden. Besonders wichtig bei der Berechnung der Biegung ist die Geometrieveränderung des Biegeträgers (z.B. Durchbiegung, Krümmung).
Zur Berechnung der Biegung und Biegebelastung wird das ursprüngliche 3D-Problem, auf einen 1D- oder auch 2D-Raum vereinfacht. Hierdurch gelingt eine näherungsweise realistische Berechnung. Die unterschiedlichen Theorien betrachten Balken oder Bögen als 1D-Körper oder Schalen und Platten als 2D-Körper. Eine nähere Beschreibung dieser Theorien findet man in diesem Skript weiter unten.
Arten der Biegung
Unterscheidung nach der Art der Belastung
Es werden zwei unterschiedliche Arten der Biegung anhand der Art der Belastung differenziert:
a) Die reine Biegung = Querkraftfreie Biegung
Hier entsteht die Biegung durch das Aufbringen zweier Biegemomente an den Enden eines Körpers / Balkens.
b) Die Querkraft-Biegung
Hier entsteht die Biegebelastung durch Kräfte, die als Querkraft auf den Balken drücken. Hier liegt neben dem entstehenden Biegemoment zusätzlich eine Querkraft vor, mit der der Biegeträger zusätzlich belastet wird. Durch sie entstehen Schubspannungen im Balken. Diese Querkraft darf bei der Berechnung nicht vergessen werden.
Unterscheidung nach dem Wirkpunkt der Belastung
Zusätzlich wird zwischen folgenden beiden Arten der Biegung unterschieden:
a) Gerade Biegung:
Biegung eines Biegeträgers / Balkens in Richtung einer der Hauptachsen des Querschnittes. Der Balken hat ein symmetrisches Profil und die Belastung erfolgt entlang einer Hauptachse des Querschnitts. Diese Biegebelastung wird als gerade Biegung bezeichnet.
b) Schiefe Biegung:
Biegung eines Biegeträgers / Balkens in eine von den Hauptachsen abweichende Richtung. Oder Biegung eines Biegeträgers / Balkens mit unsymmetrischem Querschnittsprofil.
Aus dieser Art der Biegung folgt ein zusätzliches Biegemoment in einer anderen Achse (=> My und Mz). Diese Art der Biegebelastung wird als schiefe Biegung bezeichnet.
Entstehung von Spannungen bei Biegung
Das besondere bei der Biegebelastung ist, dass hieraus sowohl Zug- als auch Druckspannungen im Biegeträger entstehen.
Zum Verständnis betrachte man hierzu einen Stab, der auf Biegung beansprucht wird. Der Stab wird nach oben gebogen, so dass er sich (in einer übertriebenen Darstellung) U-förmig verformt. Man erkennt dabei, dass der Stab an der Unterseite gedehnt wird, während er an der Oberseite gestaucht bzw. zusammengedrückt wird. Hierdurch entstehen also an der Unterseite Zugspannungen, während an der Oberseite Druckspannungen auftreten.
Verlauf von Zug- und Druckspannungen bei Biegung & die Neutrale Faser
Der Übergang von der Zug- zu Druckspannungen im Balken erfolgt jedoch nicht abrupt. Vielmehr hat man einen fließenden Übergang. Die Zug- als auch die Druckspannungen sind jeweils in den äußeren Bereichen am höchsten. Sie fallen nach innen linear ab und fallen in einer bestimmen Fläche sogar auf einen Wert von 0 (gilt für gerade Biegung). Hier ist der Übergang von Zug- auf Druckspannung. Diese Ebene, in der Zugspannung und Druckspannung gleich 0 sind, wird auch Neutrale Faser bezeichnet.
Die Neutrale Faser
Die Neutrale Faser ist also eine spannungsfrei Fläche innerhalb eines Biegeträgers. Sie trennt die Regionen innerhalb des Biegträgers, die jeweils mit Zugspannung und Druckspannung beansprucht sind.
An den Stellen, die am weitesten von der spannungsfreien Ebene (der neutralen Faser) entfernt sind, ist die Zug- bzw. Druckspannung am höchsten.
Theorien zur Berechnung der Biegung
Welche 1D- oder 2D-Biegetheorie zur Berechnung am besten eingesetzt wird hängt davon ab, ob die Biegung klein, moderat oder groß ist im Vergleich zu den Querschnittsabmessungen des Balkens / Bogens bzw. der Dicke bei Schalen und Platten.
Die bekannteste Biegetheorie ist die Balkentheorie nach Bernoulli – Bernoulli-Balken. Daneben gibt es noch die Plattentheorie nach Kirchhoff und die Plattentheorie nach von Kármán. Diese Biegetheorien werden wie folgt verwendet:
Zusammenfassung der verschiedenen Balkentheorien
- Bernoulli-Balken
= 1D-Biegetheorie => Durchbiegungen der ursprünglich geraden Mittellinie ist klein gegenüber den Querschnittsabmessungen - Plattentheorie nach Kirchhoff
= 2D-Biegetheorie => Durchbiegung der ursprünglich ebenen Mittelfläche ist klein gegenüber der Plattendicke - Plattentheorie nach von Kármán
= 2D-Biegetheorie => Durchbiegung in gleicher Größenordnung wie die Plattendicke
In diesem Mechanik-Skript wird gezeigt, wie man die Belastung auf Biegung berechnen kann. Genauer gesagt geht es hier um die Berechnung der Biegespannung eines Balkens, der mit einer Querkraft belastet wird (unterscheiden Sie hierzu die reine bzw. querkraftfreie Biegung). Zum Verständnis der Biegebelastung eines Balkens folgen hier einige wichtige Grundlagen:
Grundlagen der Biegebelastung
Sofern lange, dünne Bauteile wie etwa Wellen, Stäbe oder Balken quer zur Bauteilachse mit einem Biegemoment belastet werden, entstehen sowohl Zug- als auch Druckspannungen, aus denen letztendlich eine Durchbiegung resultiert. Wenn man diese Biegung berechnen möchte, ist folgendes Verständnis wichtig:
Im Bereich der Zugkräfte wird das betroffene Bauteil gedehnt, wogegen es in dem Bereich, in dem die Druckkräfte wirken, gestaucht wird. Die mittig zwischen diesen beiden Bereichen liegende Schicht ist die sogenannte neutrale Faser. Entlang dieser Linie findet weder eine Dehnung noch eine Stauchung statt. Laut Definition nimmt die von der neutralen Faser ausgehende Spannung in Richtung der äußeren Bauteilkante stetig immer weiter zu. Daraus resultiert, dass am äußeren Bauteilrand die stärksten Spannungen auftreten.
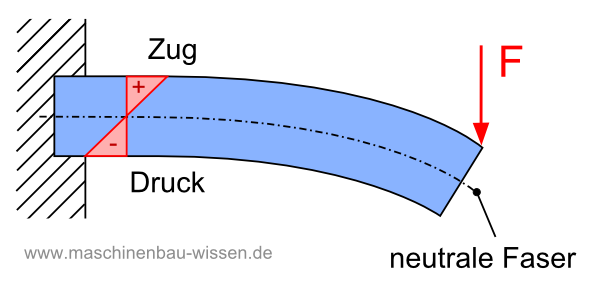
Abbildung: Biegebelastung eines Balkens mit Zug- und Druckspannungen
Mehr zum Thema Balkenbiegung finden Sie in der Hauptrubrik:
Balkenbiegung Skript
Beispiel 1 - Beanspruchung eines Bauteils auf Biegung
Der Stab, die Welle oder der Balken wird infolge der Kraft F auf Biegung beansprucht, wobei sich die ursprünglich gerade Stabachse durchbiegt. Wie ersichtlich, entstehen innerhalb des Querschnitts sowohl Zug- als auch Druckspannungen. Um diesen Sachverhalt anschaulich zu verdeutlichen, wurde der Umfang der Durchbiegung in der Skizze stark übertrieben dargestellt.
Hier noch der Hinweis, dass es sich in diesem Beispiel um eine sogenannte gerade Biegung und eine Querkraftbiegung handelt. Mehr über die unterschiedlichen Arten der Biegung lesen Sie in diesem Skript:

Abbildung: Biegebelastung eines Balkens mit Zug- und Druckspannungen
Die neutrale Faser (Strich-Punkt-Darstellung) ist vollkommen spannungslos, während an den Rändern des Stabes die stärksten Spannungen erkennbar sind. Für symmetrische Querschnitte gilt: Die Zug- und Druckspannungen verteilen sich stets linear, d. h. gleichmäßig über den gesamten Bauteilquerschnitt.
Biegespannung berechnen - Formel
Zur Berechnung der Biegespannung wird folgende Formel verwendet:
σb – Biegespannung
Mb – Biegemoment
W – Widerstandsmoment
Aus dieser Formel wird ersichtlich, dass die Biegespannung σb abhängig ist
- vom Biegemoment Mb und
- vom Widerstandsmoment W.
Wie man diese beiden Größen berechnen kann, lesen Sie im Folgenden.
Das Biegemoment Mb berechnen
Nachfolgend wurden ausschließlich Formeln für einfache Belastungsfälle angeführt. Um unübersichtliche und komplizierte Berechnungen zu vermeiden, erfolgt die Ermittlung des Biegemoments für alle anderen Fälle mittels Formeln und Tabellen, die in Tabellenbüchern zu finden sind.
In der Praxis finden sich folgende Belastungsfälle für Biegemomente Mb bei einwirkender Einzelkraft besonders häufig:
- einseitig eingespannter Träger
- Träger, der auf zwei Stützen ruht

Zwei typische Belastungsfälle für Balkenbiegung mittels Querkraft
Für den einseitig eingespannten Träger, wie er im Beispiel 1 vorliegt, gilt:
Mb – Biegemoment
F – Kraft (Querkraft)
x – Abstand (der Kraft F vom Festlager des Balkens)

Biegemoment an einem einseitig eingespannten Balken
Hier sind einige Links, in denen Sie mehr über die Grundlagen der Berechnung des Biegemoments lesen können:
- Moment, Drehmoment, Biegemoment - Grundlagen
- Moment - Beispiele
- Momentengleichgewicht – Beispiel
- Schnittreaktionen, Kräfte- & Momentengleichgewicht
- Schnittreaktionen, Kräfte- & Momentengleichgewicht - Aufgabe
Das axiale Widerstandsmoment W
Das axiale Widerstandsmoment ist ein Maß für den Widerstand gegen Durchbiegung. Deshalb wird es oft auch als Biegewiderstandsmoment bezeichnet. Für die Größe des Widerstandsmomentes ist allein die Geometrie der jeweils betrachteten Bauteil-Querschnittsfläche ausschlaggebend.
Zur Berechnung des Widerstandsmomentes ist die Definition der exakten Lage der neutralen Faser innerhalb des Querschnittes Grundvoraussetzung. Die neutrale Faser verläuft exakt durch den Schwerpunkt des Querschnitts. Ausgehend von dieser Linie lässt sich dann der größtmöglichen Abstand zur Außenkante (Randfaser) ermitteln, Dort sind die höchsten Bauteilbelastungen bzw. die größten Spannungen zu erwarten.
Das Widerstandsmoment errechnet sich als Quotient aus dem Flächenträgheitsmoment und dem Abstand (amax), der das Maß von der spannungsfreien neutralen Faser bis zur Außenkante (Randfaser) darstellt.
W – axiales Widerstandsmoment
I – axiales Flächenmoment 2. Grades (auch Flächenträgheitsmoment)
amax: größter Abstand der Randfaser zur neutralen Faser
Weiterführende Informationen über das Widerstandsmoment finden Sie in folgenden Beiträgen:
- Grundlagen Widerstandsmoment
- Widerstandsmoment & Flächenträgheitsmoment einfacher Querschnitte berechnen
- Widerstandsmoment & Flächenträgheitsmoment eines Kreisquerschnitts berechnen
- Widerstandsmoment & Flächenträgheitsmoment beliebiger Querschnitte berechnen
Das Flächenträgheitsmoment
Das Flächenträgheitsmoment (auch Flächenmoment 2. Grades) – genauer gesagt das axiale Flächenträgheitsmoment - definiert den Widerstand eines Bauteiles gegenüber Biegung. Die Berechnung erfolgt als Ableitung aus der Querschnittgeometrie des Stabes, Balkens, der Welle o. ä. Die Angabe des Flächenträgheitsmomentes erfolgt üblicherweise in der SI-Einheit m4.
Zur Berechnung des Flächenträgheitsmomentes nutzt man am besten passende Tabellen, da die eigenständige Herleitung relativ aufwändig ist.
Im Bild unten sehen Sie zwei Beispiele für die Berechnung des Flächenträgheitsmoments und des Biegewiderstandsmoments.
Mit den berechneten Größen – Biegemoment, Flächenträgheitsmoment und Widerstandsmoment – kann man nun zur zu Beginn dargestellten Formel gehen und die Biegespannung berechnen.
Weitere Skripte mit den Grundlagen des Flächenträgheitsmoments finden Sie hier:
- Grundlagen - Flächenträgheitsmoment
- Widerstandsmoment & Flächenträgheitsmoment einfacher Querschnitte berechnen
- Widerstandsmoment & Flächenträgheitsmoment eines Kreisquerschnitts berechnen
- Widerstandsmoment & Flächenträgheitsmoment beliebiger Querschnitte berechnen
Beispiel 2 - Träger ruht auf zwei Stützen
Das zweite Beispiel zeigt den zweiten typischen Fall für eine Biegebelastung. Hier kann man die Biegung relativ ähnlich berechnen.

Balken mit mittiger Querkraft belastet
Auf den auf zwei Stützen ruhenden Träger wirkt mittig die Kraft F. Das Biegemoment ergibt sich, indem der Biegequerschnitt, wie im Bild dargestellt, von der Seite betrachtet wird. Es lassen sich sowohl die Kraft F/2 als auch der Abstand x/2 erkennen. Das Biegemoment berechnet sich nun wie folgt:
Mb – Biegemoment
F – Kraft (Querkraft)
x – Abstand (der Kraft F vom Festlager des Balkens)
Das Widerstandsmoment und Flächenträgheitsmoment sind vom Biegemoment unabhängig und lassen sich genauso berechnen wie im vorhergehenden Beispiel. Mit dem Biegemoment kann dann auch die Biegespannung ermittelt werden.
Anmerkung:
Bei den hier berechneten Biegespannungen und Biegemomenten handelt es sich um die jeweils auftretenden Maximal-Werte.

Unterschiedliche Werte für Biegemoment und Biegespannung
Die Höhe des Biegemoments ist allgemein betrachtet abhängig vom Messpunkt am Balken (i.d.R. als x-Koordinate deklariert).
Die Höhe der Biegespannung ist abhängig von der Höhe des Biegemoments und somit wiederum abhängig vom Messpunkt am Balken. Betrachtet man das Innere des Balkens, ist die Biegespannung in der Randfaser mit dem größten Abstand zur neutralen Faser am höchsten. Die Biegespannung ist also auch abhängig von der Stelle innerhalb des Balkenquerschnitts, an der gemessen wird (i.d.R. die z-Koordinate).
Im folgenden Kapitel wird die querkraftfreie Biegung näher untersucht. Diese Art der Biegung wird von Experten oft auch als reine Biegung bezeichnet. Sie entsteht durch das Aufbringen von zwei Biegemomenten an den jeweiligen Enden eines Balkens. Betrachten Sie zum besseren Verständnis die Grafik unten.
Der Entscheidende Unterschied zur Querkraftbiegung ist, dass bei der reinen Biegung die Belastung nicht durch eine Querkraft verursacht wird, sondern von Momenten.
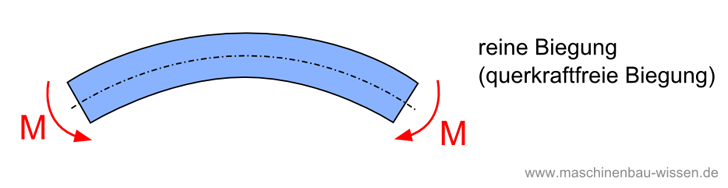
Die reine Biegung / querkraftfreie Biegung berechnen
Im ersten Schritt geht es um das Berechnen derjenigen Spannungen, die in einem beliebigen Balkenquerschnitt infolge der aufgebrachten Biegemomente entstehen. Folgende Voraussetzungen werden zugrunde gelegt:
- die Balkenschwerachse ist gerade
- im Vergleich zur Balkenlänge sind die betrachteten Balkenquerschnitte klein
- sämtliche Querschnitte bleiben während der Biegung bezüglich der Balkenachse senkrecht und eben
- im Vergleich zu den allgemeinen Abmessungen sind die durch die reine Biegung hervorgerufenen Verformungen gering
- beim Berechnen wird immer davon ausgegangen, dass sich die Spannungen im Hookeschen Bereich befinden (σ < σp)
- die Elastizitätsmodule für Zug und Druck sind identisch
- Sämtliche Lasten wirken stets auf die Hauptachse des betrachteten

Reine Biegung eines Balkens durch zwei Momenten an den Balkenenden
Wie soeben erklärt wurde, wirken sämtliche Lasten stets auf die Hauptachse des betrachteten Querschnitts - das gilt im Übrigen nicht nur für die querkraftfreie Biegung, sondern auch für die Querkraftbiegung, sodass die hier beschriebene Spannungs-Berechnungsformel für beide Fälle eingesetzt werden kann.
Lediglich bei der Berechnung des Biegemoments müssen diese beiden Arten der Biegung differenziert werden.
Die Wirkung der reinen Biegung (sowie bei allen anderen Arten der Biegung) sind demnach eine Stauchung der Balken-Oberkante und eine Dehnung der Unterkante. Während an der Oberkante also Druckspannungen in Stabrichtung wirken, sind es an der Unterkante Zugspannungen.

Betrachtet man den Balken geradlinig über den gesamten Querschnitt von oben nach unten hinweg, wechseln über die gesamte Strecke verteilt, die Spannungen von Zug über in Druck.
Als Nächstes geht es um das Berechnen der sogenannten neutrale Faser. Das ist genau die Stelle im Balkenquerschnitt, an der σ = 0 ist. Weil bei reiner Biegung im Balkenquerschnitt keine resultierende Normalkraft wirkt, kann folgender Ausdruck angewendet werden:
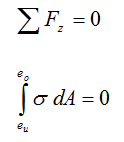
Der Index z bezieht sich hierbei auf die Richtung der Balkenachse.
Weil für das Berechnen der reinen Biegung die angenommene Ebenheit aller Querschnitte bei Verformung Grundvoraussetzung ist, gilt:
Es folgt:
Dieses Berechnungsschema besitzt jedoch nur dann Gültigkeit, wenn sich der zur Integration erforderliche Ursprung in der Schwerpunktachse des Balkens befindet. Anders ausgedrückt: Die Ermittlung der neutralen Faser erfolgt immer vom Schwerpunkt der Balkenquerschnitts aus (bzw. der Schwerachse).
Die Schwerachse des Balkens ist somit identisch zur neutralen Faser, auf der die Biegespannung = 0 wird.
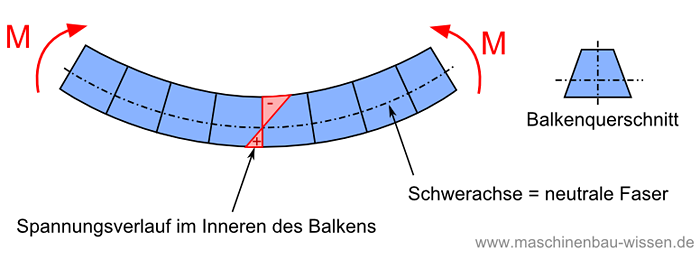 Schwerachse bzw. neutrale Faser
Schwerachse bzw. neutrale Faser
Sofern das aufgebrachte Biegemoment bekannt ist, lässt sich die daraus resultierende Spannung entlang des Querschnittes σ = σ(z) relativ einfach berechnen. Wichtig ist dabei allerdings die Annahme, dass in jedem Querschnitt des Balkens nicht nur ein Kräftegleichgewicht, sondern auch ein Momentengleichgewicht gewährleistet ist. Der vorhergehenden Darstellung zufolge gilt demnach:
M - Biegemoment
Iyy – Flächenträgheitsmoment
E – Elastizitätsmodul
σ – Biegespannung
Die Größe Iyy wird auch als das Flächenträgheitsmoment eines Balkens bei Biegung um die y-Achse bezeichnet. Diese Größe ist für jeden Flächenquerschnitt neu zu berechnen. Seine Dimension ist m4.
Diese Berechnung erfolgt bei elementaren Querschnitten, wie etwa Kreisen oder Rechtecken mithilfe direkter Integration oder noch einfacher per vorgefertigter Berechnungsformeln, falls man diese zur Hand hat. Das kann bei zusammengesetzten Körpern sehr unübersichtlich und kompliziert werden. Deshalb bedient man sich bei der Berechnung des Flächenträgheitsmoments zusammengesetzter Körper zumeist einer erweiterten Tabellenkalkulation.
Der Index "yy" bedeutet, dass es sich um eine Biegung um die y-y-Achse handelt. Das muss allerdings nicht immer der Fall sein. Theoretisch könnte sich der Körper auch um seine z-z-Achse biegen. Allerdings müsste die Berechnung des Flächenträgheitsmomentes dann anders erfolgen, nämlich:
Zusammenfassung
Berechnung der Spannung bei reiner Biegung
Biegespannung berechnen allgemein:
Biegespannung in der oberen Randfaser berechnen:
Biegespannung in der unteren Randfaser berechnen:
Die Angaben für die obere und untere Randspannung (eo, eu) werden hierbei als bekannt vorausgesetzt.
Berechnung des Widerstandsmoments bei reiner Biegung
Eine Definition des Widerstandsmomentes Wy eines Balkens erfolgt mit:
Widerstandsmoment in der oberen Randfaser berechnen:
Widerstandsmoment in der unteren Randfaser berechnen:
Folgerung:
Alternativ lässt sich demnach für die Berechnung der Biegespannung schreiben:
Merke:
- Trägheitsmomente beziehen sich immer auf ein und dieselbe Schwerachse und besitzen somit für den gesamten Querschnitt (A) Gültigkeit
- Widerstandsmomente beziehen sich dagegen auf einen speziellen Querschnittpunkt bzw. auf eine Linie, die sich immer in gleichem Abstand zur Schwerachse befindet
- die größte Spannung tritt stets an der Stelle des kleinsten Widerstandsmomentes auf
- in den meisten Tabellen, die für querkraftfreie Biegung herangezogen werden, ist von vornherein nur das kleinste Widerstandsmoment (Wmin) aufgeführt
- Obwohl die Widerstandsmomente aufgrund ihres jeweiligen Abstandsmaßes eigentlich mit einem entweder positiven oder negativen Vorzeichen belegt sein müssten, finden sich in den Regelwerken und Handbüchern zum Thema "reine Biegung" keine Vorzeichenangaben.
Im Unterschied zur bisher betrachteten reinen Biegung, kommt bei der Querkraftbiegung zusätzlich zum Biegemoment noch eine weitere Kraft - die Querkraft - hinzu.
Die untere Abbildung zeigt ein exemplarisches Beispiel: Hier wirkt auf einen einseitig eingespannten Balken eine Querkraft. Diese Querkraft führt letztendlich zu Schubspannungen. Die entsprechende Berechnung dazu findet sich im Kapitel weiter unten.
 Einseitig eingespannter Balken mit Querkraft F belastet
Einseitig eingespannter Balken mit Querkraft F belastet
Die Normalspannungen im Balken infolge Querkraftbiegung
Anmerkung: Bei der Berechnung der Normalspannungen wurde davon ausgegangen, dass die dargestellten Schubspannungen keinen Einfluss auf den Träger bzw. Balken (immer ein gleichbleibendes bzw. wenig veränderliches Profil vorausgesetzt) haben. Anders ausgedrückt: Sofern die Abmessungen des Balkenquerschnitts im Vergleich zu seiner Länge klein sind, dürfen die durch die Schubspannungen hervorgerufenen "Verwölbungen", vernachlässigt werden.
Unter Querkraftbiegung ist die Spannung bei einem gleichbleibenden Balkenquerschnitt die Spannung nicht überall gleich. In unserem einfachen Beispiel mit einer Querkraft nimmt die Randspannung zu, je größer der Abstand zu Kraft wird (siehe Hebelgesetze). Aus diesem Grund ist es hier möglich den Balken abgestuft oder mit stetig veränderlichem Querschnitt auszuführen. Eine derartige Optimierung kann zum Beispiel Gewicht, Material und/oder Kosten sparen.
Die folgende Grafik zeigt den Biegemomentenverlauf in einem einseitig fest eingespannten Balken aufgrund einer Querkraft am freien Balkenende.
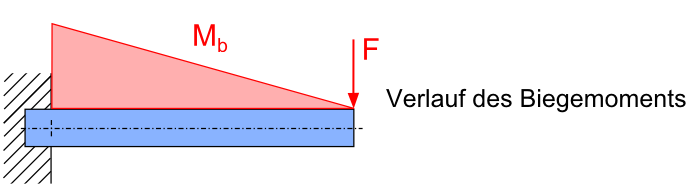
Biegemomentenverlauf bei Querkraftbiegung
In diesem Sinne wollen wir nun die Querschnittsform eins Balkens (bzw. Trägers) berechnen, der an jeder Stelle unter der gleichen Randspannung steht. Der Träger ist somit ideal dimensioniert. Als Grundform verwenden wir einen rechteckigen Querschnitt b x h(x):
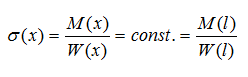
Mit einer weiteren Rechnung ergibt sich erforderliche Balkenform (eine Parabel), die der angenommenen Belastung ideal standhält:

Betrachtet man den Balken rein konstruktiv, wird schnell ersichtlich, dass die Höhe h(x) auch bei schwindender Querkraft niemals null werden kann. Zur Darstellung der Querkraftbiegung verwendet man deshalb in der Praxis zumeist Trapezformen. Damit ist eine Annäherung an einen Balken mit gleicher Randspannung am besten gewährleistet. Ein anschauliches Beispiel liefert folgende Abbildung:
Wie man das Flächenträgheitsmoment und Widerstandsmoment für unterschiedliche Balken-Querschnitte berechnen kann, ist in den anderen Skripten auf dieser Website ausführlich erklärt.
Achtung! Was man bei der Querkraftbiegung jedoch nicht außer Acht lassen darf ist die Querkraft selbst. In unserem einfachen Beispiel (einseitig fest eingespannter Balken mit Querkraft am freien Ende) wirkt diese Querkraft konstant über die gesamte Länge des Balkens.
Das Maß eines bestimmten Widerstandes gegen eine Biegung wird als axiales Widerstandsmoment oder auch als Biegewiderstandsmoment bezeichnet. Es wird zur Berechnung von mechanischen Spannungen bei Biegebelastung benötigt. Diese Berechnungen benötigen Konstrukteure und Techniker, um Aussagen über die Steifigkeit und Durchbiegung geometrischer Körper bei bestimmten Belastungen, wie sie beispielsweise bei der einseitigen Biegung um eine Achse auftreten, treffen zu können.
Ein wesentlicher Faktor für die Höhe des Biegewiderstandsmoments ist die Geometrie des Balken-Querschnitts und auch die Richtung der Biegebelastung. Bei günstiger Belastungsrichtung ist die Durchbiegung deutlich geringer, als bei einer ungünstigen Belastungsrichtung.
Betrachten Sie hierzu die Darstellung unten.

Biegebelastung aus unterschiedlicher Richtung bei gleicher Querschnittsgeometrie
Die folgende Grafik zeigt die Verformung und den Spannungsverlauf bei der Biegung eines Balkens. Wie man darauf bereits erkennen kann, sind die Verformung und die mechanische Spannung abhängig von der Querschnittsgeometrie des Balkens. Hierzu jedoch Näheres im weiteren Verlauf dieses Tutorials.

Verformung und Spannung bei der Biegebelastung eines Balkens
Berechnung des axialen Widerstandsmoments
Das axiale Widerstandsmoment wird bei einer Biegebelastung mit folgender Gleichung berechnet:
W – axiales Widerstandsmoment
I – axiales Flächenmoment 2. Grades (auch Flächenträgheitsmoment)
amax: größter Abstand der Randfaser zur neutralen Faser
Das Flächenträgheitsmoment I wird durch die Geometrie des Querschnitts des belasteten Balkens definiert. Wie man das Flächenträgheitsmoment berechnet und wie sich diese Berechnung herleiten lässt, lesen Sie im Folgenden.
Berechnung & Herleitung des Flächenträgheitsmomentes
Nachfolgend soll für einen einfachen Querschnitt sowohl das Flächenträgheitsmoment als auch das Widerstandsmoment berechnet werden.
Eigentlich wäre hierfür die Berechnung des zweifachen Integrals über die Querschnittsfläche A (zweidimensional) notwendig. Durch die zweckmäßige Auswahl der Integrationsvariablen lässt sich jedoch für manche Anwendungen die komplizierte Doppelintegration umgehen und die gesamte Berechnung auf ein eindimensionales Integral zurückführen. Hier ein Beispiel:
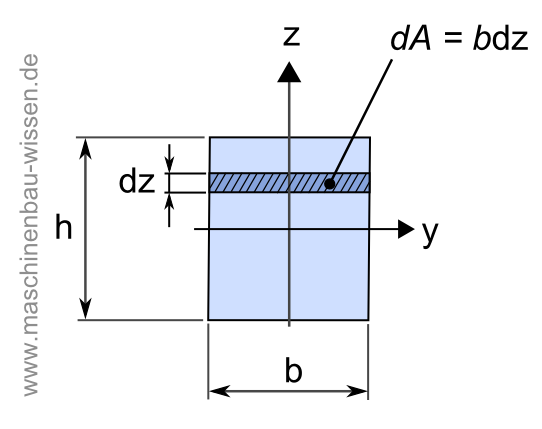
Querschnitt eines Balkens
Die folgende Abbildung zeigt eine rechteckige Querschnittsfläche eines Balkens mit Höhe h und Breite b. Das zugehörige Flächenträgheitsmoment ergibt sich aus der folgenden Berechnung.
Berechnung des Flächenträgheitsmoments bei Biegung um die y-Achse:
Iyy - Flächenträgheitsmoments bei Biegung um die y-Achse
z – Länge auf der z-Achse (Höhe)
A – Fläche des Querschnitts
Aus dieser allgemeinen Formel kann man nun die spezifische Berechnung für unseren Balkenquerschnitt herleiten. Hierzu muss man das Integral entsprechend lösen.
Zunächst gilt für die Fläche A des Balkenquerschnitts:
Durch einsetzen und integrieren ergibt sich folgende Gleichung:
Aus Gründen der Symmetrie befindet sich im dargestellten Beispiel die Schwerachse exakt in der Mitte des Rechteck-Querschnittes, denn es gilt ja als vereinbart, dass sich das Flächenträgheitsmoment auf die Balken-Schwerachse bezieht. Diese Annahme muss nun bei der Integration entsprechend berücksichtigt werden. Deshalb kann nun mit der Formel
ohne weitere Umwege das Widerstandsmoment für einen Balken berechnet werden, der über einen rechteckigen Querschnitt verfügt.
Bemerkung zum Abschluss:
Das Trägheitsmoment, Widerstandsmoment und Biegewiderstandsmoment für bestimmte Walzprofile lässt sich vergleichsweise unkompliziert anhand von Tabellen ermitteln.



