Die Definition des Widerstandsmoments allgemein und des Biegewiderstandsmoments im Speziellen, haben wir bereits in vorhergehenden Skripten beschrieben. Hier lernen Sie nun, wie man das Biegewiderstandsmoments eines Stabs mit Kreisquerschnitt berechnen kann.

Berechnung des Widerstandsmoments eines Stabs mit Kreisquerschnitt

1. Herleitung & Berechnung des Flächenträgheitsmomentes eines Kreises

Bevor man das Widerstandsmoment berechnen kann, muss zunächst das Flächenträgheitsmoment des jeweiligen Stab-Querschnitts ermittelt werden. Wesentlich für die Berechnung ist die Belastungsrichtung – handelt es sich z.B. um eine Biegebelastung um die y- oder z-Achse?

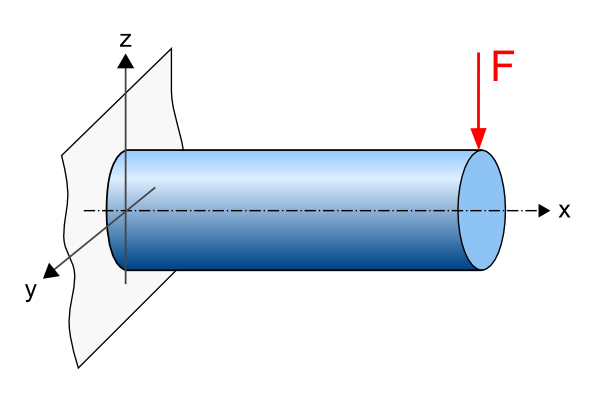
Biegung eines Stabes um die y-Achse

Im folgenden beispielhaften Fall liegt eine Biegebelastung um die y-Achse vor. Die allgemeine Berechnungsformel des Flächenträgheitsmoments sieht demnach wie folgt aus:

I_yy - Flächenträgheitsmoments bei Biegung um die y-Achse
z – Länge auf der z-Achse (Höhe)
A – Fläche des Querschnitts

Aus dieser allgemeinen Formel kann man nun die spezifische Berechnung für unseren Kreisquerschnitt herleiten. Hierzu muss man das Integral entsprechend lösen.

Lösung des Integrals zur Berechnung des Flächenträgheitsmoments eine Kreisfläche

Die folgenden Berechnungen beziehen sich auf das Flächenträgheitsmoment und das Widerstandsmoment für die in der unteren Abbildung dargestellten Kreisfläche. Zunächst erfolgt die Rechnung analog zum Fall des Rechteck-Querschnitts aus dem vorhergehenden Tutorial.

Querschnittsfläche des Biegebalkens

Die Fläche des Kreissegments, die wir für die Berechnung des Flächenträgheitsmomentes benötigen, berechnet sich allgemein ausgedrückt wie in der folgenden Gleichung. Die y-Koordinate für die Flächenberechnung ergibt sich außerdem durch den Satz von Pythagoras mit dem Faktor 2 multipliziert.

Mit dieser Formel ergibt sich die Berechnung des Flächenträgheitsmomentes wie folgt:

I_yy - Flächenträgheitsmoments bei Biegung um die y-Achse
z – Länge auf der z-Achse (Höhe)
A – Fläche des Querschnitts
D- Kreisdurchmesser
r – Radius des Kreises
π – Kreiszahl (3,14159…)

1. Berechnung des Widerstandsmoments der Kreisquerschnittsfläche

Mit Hilfe des Flächenträgheitsmomentes kann man nun das Widerstandsmoment gegen Biegung relativ einfach berechnen.

Die allgemeine Formel lautet:

W – axiales Widerstandsmoment
I – axiales Flächenmoment 2. Grades (auch Flächenträgheitsmoment)
a_max: größter Abstand der Randfaser zur neutralen Faser

Für unseren Fall – Biegung um die y-Achse – kann man die Formel wie folgt spezifisch ausdrücken:

Für die in der obigen Abbildung dargestellten achsfernen Punkte u und o wird das Widerstandsmoment folgendermaßen ermittelt:

Somit hat man das Widerstandsmoment für den Kreisquerschnitt ermittelt. Dieses Beispiel soll einfach zeigen, wie man die entsprechenden Berechnungsformeln herleiten kann.
Steht man in der Realität vor der Aufgabe die Biegung eines Profils zu berechnen, wird man normaler Wiese die Formeln aus Tabellen entnehmen. Man fängt hier natürlich nicht an, alles von Null an herzuleiten.