Im folgenden Kapitel wird die querkraftfreie Biegung näher untersucht. Diese Art der Biegung wird von Experten oft auch als reine Biegung bezeichnet. Sie entsteht durch das Aufbringen von zwei Biegemomenten an den jeweiligen Enden eines Balkens. Betrachten Sie zum besseren Verständnis die Grafik unten.

Der Entscheidende Unterschied zur Querkraftbiegung ist, dass bei der reinen Biegung die Belastung nicht durch eine Querkraft verursacht wird, sondern von Momenten.

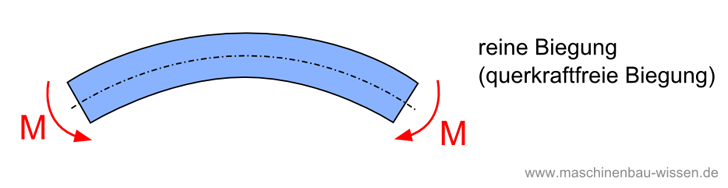
Die reine Biegung / querkraftfreie Biegung berechnen
 

Im ersten Schritt geht es um das Berechnen derjenigen Spannungen, die in einem beliebigen Balkenquerschnitt infolge der aufgebrachten Biegemomente entstehen. Folgende Voraussetzungen werden zugrunde gelegt:

- die Balkenschwerachse ist gerade
- im Vergleich zur Balkenlänge sind die betrachteten Balkenquerschnitte klein
- sämtliche Querschnitte bleiben während der Biegung bezüglich der Balkenachse senkrecht und eben
- im Vergleich zu den allgemeinen Abmessungen sind die durch die reine Biegung hervorgerufenen Verformungen gering
- beim Berechnen wird immer davon ausgegangen, dass sich die Spannungen im Hookeschen Bereich befinden (σ < σ_p)
- die Elastizitätsmodule für Zug und Druck sind identisch
- Sämtliche Lasten wirken stets auf die Hauptachse des betrachteten

Reine Biegung eines Balkens durch zwei Momenten an den Balkenenden
 

Wie soeben erklärt wurde, wirken sämtliche Lasten stets auf die Hauptachse des betrachteten Querschnitts - das gilt im Übrigen nicht nur für die querkraftfreie Biegung, sondern auch für die Querkraftbiegung, sodass die hier beschriebene Spannungs-Berechnungsformel für beide Fälle eingesetzt werden kann.
Lediglich bei der Berechnung des Biegemoments müssen diese beiden Arten der Biegung differenziert werden.

Die Wirkung der reinen Biegung (sowie bei allen anderen Arten der Biegung) sind demnach eine Stauchung der Balken-Oberkante und eine Dehnung der Unterkante. Während an der Oberkante also Druckspannungen in Stabrichtung wirken, sind es an der Unterkante Zugspannungen.

Betrachtet man den Balken geradlinig über den gesamten Querschnitt von oben nach unten hinweg, wechseln über die gesamte Strecke verteilt, die Spannungen von Zug über in Druck.

Als Nächstes geht es um das Berechnen der sogenannten neutrale Faser. Das ist genau die Stelle im Balkenquerschnitt, an der σ = 0 ist. Weil bei reiner Biegung im Balkenquerschnitt keine resultierende Normalkraft wirkt, kann folgender Ausdruck angewendet werden:

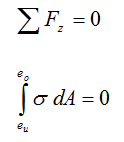
Der Index z bezieht sich hierbei auf die Richtung der Balkenachse.

Weil für das Berechnen der reinen Biegung die angenommene Ebenheit aller Querschnitte bei Verformung Grundvoraussetzung ist, gilt:

Es folgt:

Dieses Berechnungsschema besitzt jedoch nur dann Gültigkeit, wenn sich der zur Integration erforderliche Ursprung in der Schwerpunktachse des Balkens befindet. Anders ausgedrückt: Die Ermittlung der neutralen Faser erfolgt immer vom Schwerpunkt der Balkenquerschnitts aus (bzw. der Schwerachse).
Die Schwerachse des Balkens ist somit identisch zur neutralen Faser, auf der die Biegespannung = 0 wird.

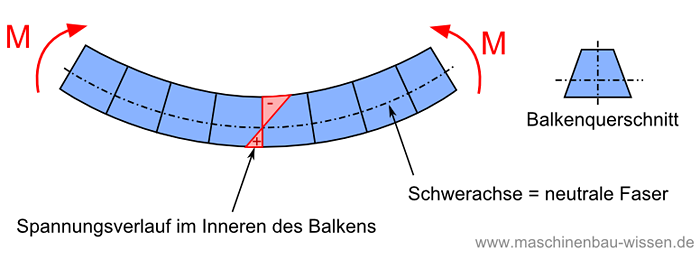Schwerachse bzw. neutrale Faser
 

Sofern das aufgebrachte Biegemoment bekannt ist, lässt sich die daraus resultierende Spannung entlang des Querschnittes σ = σ(z) relativ einfach berechnen. Wichtig ist dabei allerdings die Annahme, dass in jedem Querschnitt des Balkens nicht nur ein Kräftegleichgewicht, sondern auch ein Momentengleichgewicht gewährleistet ist. Der vorhergehenden Darstellung zufolge gilt demnach:

M - Biegemoment
I_yy – Flächenträgheitsmoment
E – Elastizitätsmodul
σ – Biegespannung

Die Größe I_yy wird auch als das Flächenträgheitsmoment eines Balkens bei Biegung um die y-Achse bezeichnet. Diese Größe ist für jeden Flächenquerschnitt neu zu berechnen. Seine Dimension ist m⁴.
Diese Berechnung erfolgt bei elementaren Querschnitten, wie etwa Kreisen oder Rechtecken mithilfe direkter Integration oder noch einfacher per vorgefertigter Berechnungsformeln, falls man diese zur Hand hat. Das kann bei zusammengesetzten Körpern sehr unübersichtlich und kompliziert werden. Deshalb bedient man sich bei der Berechnung des Flächenträgheitsmoments zusammengesetzter Körper zumeist einer erweiterten Tabellenkalkulation.

Der Index "yy" bedeutet, dass es sich um eine Biegung um die y-y-Achse handelt. Das muss allerdings nicht immer der Fall sein. Theoretisch könnte sich der Körper auch um seine z-z-Achse biegen. Allerdings müsste die Berechnung des Flächenträgheitsmomentes dann anders erfolgen, nämlich:

Zusammenfassung

Berechnung der Spannung bei reiner Biegung

Biegespannung berechnen allgemein:

Biegespannung in der oberen Randfaser berechnen:

Biegespannung in der unteren Randfaser berechnen:

Die Angaben für die obere und untere Randspannung (e_o, e_u) werden hierbei als bekannt vorausgesetzt.

Berechnung des Widerstandsmoments bei reiner Biegung

Eine Definition des Widerstandsmomentes W_y eines Balkens erfolgt mit:

Widerstandsmoment in der oberen Randfaser berechnen:

Widerstandsmoment in der unteren Randfaser berechnen:

Folgerung:

Alternativ lässt sich demnach für die Berechnung der Biegespannung schreiben:

Merke:

• Trägheitsmomente beziehen sich immer auf ein und dieselbe Schwerachse und besitzen somit für den gesamten Querschnitt (A) Gültigkeit
• Widerstandsmomente beziehen sich dagegen auf einen speziellen Querschnittpunkt bzw. auf eine Linie, die sich immer in gleichem Abstand zur Schwerachse befindet
• die größte Spannung tritt stets an der Stelle des kleinsten Widerstandsmomentes auf
• in den meisten Tabellen, die für querkraftfreie Biegung herangezogen werden, ist von vornherein nur das kleinste Widerstandsmoment (W_min) aufgeführt
• Obwohl die Widerstandsmomente aufgrund ihres jeweiligen Abstandsmaßes eigentlich mit einem entweder positiven oder negativen Vorzeichen belegt sein müssten, finden sich in den Regelwerken und Handbüchern zum Thema "reine Biegung" keine Vorzeichenangaben.