Im Unterschied zur bisher betrachteten reinen Biegung, kommt bei der Querkraftbiegung zusätzlich zum Biegemoment noch eine weitere Kraft - die Querkraft - hinzu.

Die untere Abbildung zeigt ein exemplarisches Beispiel: Hier wirkt auf einen einseitig eingespannten Balken eine Querkraft. Diese Querkraft führt letztendlich zu Schubspannungen. Die entsprechende Berechnung dazu findet sich im Kapitel weiter unten.

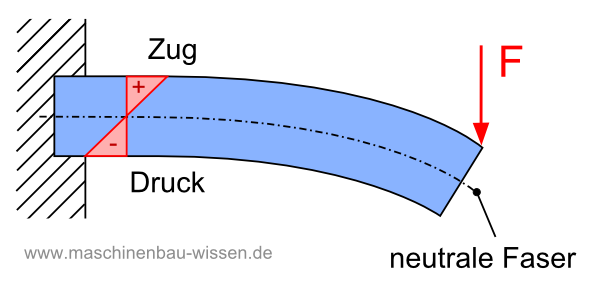Einseitig eingespannter Balken mit Querkraft F belastet
 

Die Normalspannungen im Balken infolge Querkraftbiegung

Anmerkung: Bei der Berechnung der Normalspannungen wurde davon ausgegangen, dass die dargestellten Schubspannungen keinen Einfluss auf den Träger bzw. Balken (immer ein gleichbleibendes bzw. wenig veränderliches Profil vorausgesetzt) haben. Anders ausgedrückt: Sofern die Abmessungen des Balkenquerschnitts im Vergleich zu seiner Länge klein sind, dürfen die durch die Schubspannungen hervorgerufenen "Verwölbungen", vernachlässigt werden.

Unter Querkraftbiegung ist die Spannung bei einem gleichbleibenden Balkenquerschnitt die Spannung nicht überall gleich. In unserem einfachen Beispiel mit einer Querkraft nimmt die Randspannung zu, je größer der Abstand zu Kraft wird (siehe Hebelgesetze). Aus diesem Grund ist es hier möglich den Balken abgestuft oder mit stetig veränderlichem Querschnitt auszuführen. Eine derartige Optimierung kann zum Beispiel Gewicht, Material und/oder Kosten sparen.

Die folgende Grafik zeigt den Biegemomentenverlauf in einem einseitig fest eingespannten Balken aufgrund einer Querkraft am freien Balkenende.

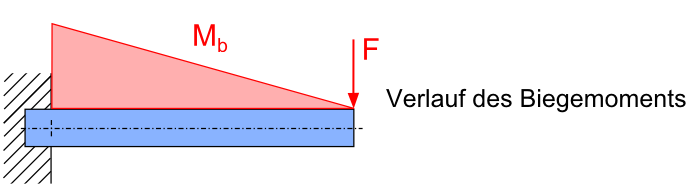
Biegemomentenverlauf bei Querkraftbiegung
 

In diesem Sinne wollen wir nun die Querschnittsform eins Balkens (bzw. Trägers) berechnen, der an jeder Stelle unter der gleichen Randspannung steht. Der Träger ist somit ideal dimensioniert. Als Grundform verwenden wir einen rechteckigen Querschnitt b x h(x):

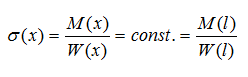
Mit einer weiteren Rechnung ergibt sich erforderliche Balkenform (eine Parabel), die der angenommenen Belastung ideal standhält:

Betrachtet man den Balken rein konstruktiv, wird schnell ersichtlich, dass die Höhe h(x) auch bei schwindender Querkraft niemals null werden kann. Zur Darstellung der Querkraftbiegung verwendet man deshalb in der Praxis zumeist Trapezformen. Damit ist eine Annäherung an einen Balken mit gleicher Randspannung am besten gewährleistet. Ein anschauliches Beispiel liefert folgende Abbildung:

Wie man das Flächenträgheitsmoment und Widerstandsmoment für unterschiedliche Balken-Querschnitte berechnen kann, ist in den anderen Skripten auf dieser Website ausführlich erklärt.

Achtung! Was man bei der Querkraftbiegung jedoch nicht außer Acht lassen darf ist die Querkraft selbst. In unserem einfachen Beispiel (einseitig fest eingespannter Balken mit Querkraft am freien Ende) wirkt diese Querkraft konstant über die gesamte Länge des Balkens.