Mechanik - Festigkeitslehre

Torsionsbeanspruchung bedeutet in der Technischen Mechanik*, dass ein Bauteil wie Stab oder Welle mit einem Moment (Drehmoment bzw. Torsionsmoment) belastet wird, welches um deren Längsachse wirkt. Im Bereich der Torsionsbeanspruchung haben wir es überwiegend mit kreisförmigen Bauteilen zu tun, weil gerade diese besonders für die Übertragung großer Drehmomente geeignet sind.

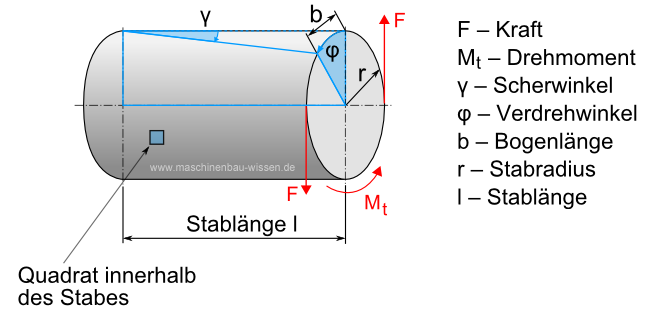
Bei der Beanspruchung auf Torsion, kommt es zu einem schraubenförmigen Verformen. Diese Verformung kann man in der Grafik anhand der dargestellten Linien auf der Mantelfläche des Stabes erkennen. Aufgrund dessen verformt sich ein quadratisches Element auf der Oberfläche des Stabes zu einer Raute, deren senkrechte wie auch radiale Linen unverformt bleiben.

Wie berechnet man nun die Torsion? Wir erhalten das Torsionsmoment M_t, indem wir die Kraft F mit Länge r des eingesetzten Hebels multiplizieren.

M_t – Torsionsmoment
F – Kraft
r – Hebelarm = Stabradius

Dies ist das Drehmoment – die Berechnung der Spannung und Verformung erfolgt in den nächsten Schritten.

Den Verdrehwinkel berechnen

Das Einwirken des Torsionsmoments Mt hat den Effekt, dass das betreffende Bauteil um den Verdrehwinkel φ verdreht, sowie um den Scherwinkel γ verzerrt wird.
Den Verdrehwinkel des Stabs berechnet man aus dem Torsionsmoment T geteilt durch das Torsionsträgheitsmoment I_T, welches die Größe und Form des Stabquerschnitts beschreibt, und den Schubmodul G, multipliziert mit der Stablänge l:

φ – Verdrehwinkel
T – Torsionsmoment
l – Stablänge
G – Schubmodul
I_T – Torsionsträgheitsmoment

Den Scherwinkel berechnen

Wenn man den Verdrehwinkel φ mit dem Radius r multipliziert, ergibt sich die Bogenlänge b, die Sie ebenfalls durch Multiplikation von Scherwinkel γ und Stablänge l erhalten - Winkelangaben werden im Bogenmaß (Radiant) angegeben. Der Verdrehwinkel zeigt sich proportional zur Länge des Stabes, der Scherwinkel zum Radius proportional. Insofern steht der Verdrehwinkel in konkretem Zusammenhang mit dem Scherwinkel. Aus diesen Erkenntnissen lässt sich also folgende Gleichung für die Berechnung ableiten:

b – Bogenlänge
γ – Scherwinkel
l – Stablänge
φ – Verdrehwinkel
r – Stabradius

Wenn man die Bogenlänge b aus der Gleichung eliminiert und auf den Scherwinkel γ umstellt, erhält man die folgende Gleichung, mit der man den Scherwinkel berechnen kann.

Die Berechnung des Scherwinkels funktioniert auch mit Hilfe von Torsionsmoment, polarem Widerstandsmoment und Schubmodul:

Mt – Torsionsmoment
Wp – polares Widerstandsmoment
G – Schubmodul

Es erben sich aus dieser Feststellung folgende weitere Zusammenhänge:

Die Schubspannung infolge von Torsion berechnen

Ein Torsionsträgheitsmoment entspricht nur für geschlossene Kreisringquerschnitte und Kreisquerschnitte dem polaren Flächenträgheitsmoment I_T = I_p. Was die Torsion anderer Querschnitte betrifft, lässt sich die Berechnung eines Torsionsträgheitsmoments lediglich in spezifischen Fällen bei geschlossener Form realisieren. Hinsichtlich der Bestimmung ist in zahlreichen Fällen folgende Frage relevant: Haben wir hier verwölbungsfreie Querschnitte? Wird die Verwölbung blockiert oder nicht?

Bei gleichmäßigen Querschnitten, wo sich Produkte aus Radius und Wandstärke über der Laufvariablen konstant zeigen und wir es mit einem geschlossenen Profil zu tun haben, treten bei einer Torsion keine Spannungen in Längsrichtung - und so keine Verwölbung des Querschnitts - auf.

Sie berechnen die Schubspannung τ_t im Stab, indem Sie Torsionsmoment M_t durch polares Widerstandsmoment W_p teilen:

Das polare Widerstandmoment berechnet sich aus folgender Formel* :

a_max - größter Abstand der Randfaser zur neutralen Faser [m]

Im Falle eines runden Stabes ist amax der Radius r. Womit die Gleichung der Schubspannung wie folgt aussieht:

Es erben sich aus dieser Feststellung folgende weitere Zusammenhänge:

Beachten Sie bei Ihrer Berechnung, dass diese Schubspannung die Schubspannung τ_zul, wie sie für das zu verwendende Material maximal zulässig ist, nicht überschreiten darf.

τ_t ≤ τ_zul

Eine zu starke Verdrehung bzw. Torsion führt dazu, dass die Verformung - etwa einer Welle - vom elastischen Bereich in den plastischen übergeht, was letztendlich zum Bruch infolge der Torsionsbeanspruchung führt.