Das Maß eines bestimmten Widerstandes gegen eine Biegung wird als axiales Widerstandsmoment oder auch als Biegewiderstandsmoment bezeichnet. Es wird zur Berechnung von mechanischen Spannungen bei Biegebelastung benötigt. Diese Berechnungen benötigen Konstrukteure und Techniker, um Aussagen über die Steifigkeit und Durchbiegung geometrischer Körper bei bestimmten Belastungen, wie sie beispielsweise bei der einseitigen Biegung um eine Achse auftreten, treffen zu können.

Ein wesentlicher Faktor für die Höhe des Biegewiderstandsmoments ist die Geometrie des Balken-Querschnitts und auch die Richtung der Biegebelastung. Bei günstiger Belastungsrichtung ist die Durchbiegung deutlich geringer, als bei einer ungünstigen Belastungsrichtung.
Betrachten Sie hierzu die Darstellung unten.

Biegebelastung aus unterschiedlicher Richtung bei gleicher Querschnittsgeometrie

Die folgende Grafik zeigt die Verformung und den Spannungsverlauf bei der Biegung eines Balkens. Wie man darauf bereits erkennen kann, sind die Verformung und die mechanische Spannung abhängig von der Querschnittsgeometrie des Balkens. Hierzu jedoch Näheres im weiteren Verlauf dieses Tutorials.

Verformung und Spannung bei der Biegebelastung eines Balkens

Berechnung des axialen Widerstandsmoments

Das axiale Widerstandsmoment wird bei einer Biegebelastung mit folgender Gleichung berechnet:

W – axiales Widerstandsmoment
I – axiales Flächenmoment 2. Grades (auch Flächenträgheitsmoment)
a_max: größter Abstand der Randfaser zur neutralen Faser

Das Flächenträgheitsmoment I wird durch die Geometrie des Querschnitts des belasteten Balkens definiert. Wie man das Flächenträgheitsmoment berechnet und wie sich diese Berechnung herleiten lässt, lesen Sie im Folgenden.

Berechnung & Herleitung des Flächenträgheitsmomentes

Nachfolgend soll für einen einfachen Querschnitt sowohl das Flächenträgheitsmoment als auch das Widerstandsmoment berechnet werden.

Eigentlich wäre hierfür die Berechnung des zweifachen Integrals über die Querschnittsfläche A (zweidimensional) notwendig. Durch die zweckmäßige Auswahl der Integrationsvariablen lässt sich jedoch für manche Anwendungen die komplizierte Doppelintegration umgehen und die gesamte Berechnung auf ein eindimensionales Integral zurückführen. Hier ein Beispiel:

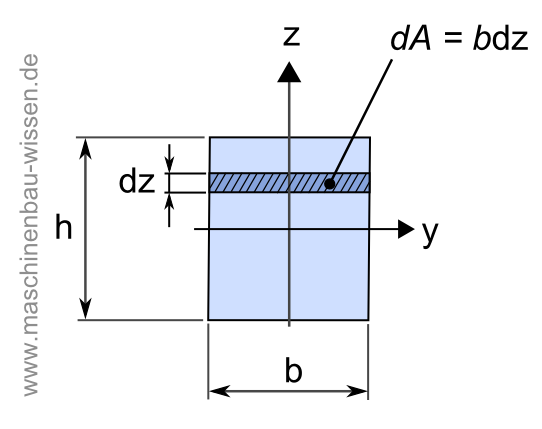
Querschnitt eines Balkens

Die folgende Abbildung zeigt eine rechteckige Querschnittsfläche eines Balkens mit Höhe h und Breite b. Das zugehörige Flächenträgheitsmoment ergibt sich aus der folgenden Berechnung.

Berechnung des Flächenträgheitsmoments bei Biegung um die y-Achse:

I_yy - Flächenträgheitsmoments bei Biegung um die y-Achse
z – Länge auf der z-Achse (Höhe)
A – Fläche des Querschnitts

Aus dieser allgemeinen Formel kann man nun die spezifische Berechnung für unseren Balkenquerschnitt herleiten. Hierzu muss man das Integral entsprechend lösen.

Zunächst gilt für die Fläche A des Balkenquerschnitts:

Durch einsetzen und integrieren ergibt sich folgende Gleichung:

Aus Gründen der Symmetrie befindet sich im dargestellten Beispiel die Schwerachse exakt in der Mitte des Rechteck-Querschnittes, denn es gilt ja als vereinbart, dass sich das Flächenträgheitsmoment auf die Balken-Schwerachse bezieht. Diese Annahme muss nun bei der Integration entsprechend berücksichtigt werden. Deshalb kann nun mit der Formel

ohne weitere Umwege das Widerstandsmoment für einen Balken berechnet werden, der über einen rechteckigen Querschnitt verfügt.

Bemerkung zum Abschluss:
Das Trägheitsmoment, Widerstandsmoment und Biegewiderstandsmoment für bestimmte Walzprofile lässt sich vergleichsweise unkompliziert anhand von Tabellen ermitteln.