In diesem Skript geht es um die Berechnung des Widerstandsmoments und Flächenträgheitsmoments von beliebig zusammengesetzten Querschnitten.

Dieses Kapitel geht von der Annahme aus, dass die Trägheitsmomente sämtlicher Teilflächen, aus denen sich ein bestimmter Körper zusammensetzt, zunächst einmal bekannt sind und dass es sich dabei beispielsweise um Kreise, Rechtecke oder gewalzte Profile handelt.

Berechnung von Trägheitsmoment & Widerstandsmoment bei gemeinsamer Schwerachse

Welche Möglichkeit gibt es nun, das Widerstandsmoment und das Trägheitsmoment aus den einzelnen Körpern zu berechnen, um sie dann auf den gesamten Körper zu beziehen? Hierfür wird in einem ersten Schritt angenommen, dass sich die Schwerpunkte aller Teilkörper, so wie in der folgenden Abbildung dargestellt, auf einer gemeinsamen Achse, der sogenannten Schwerachse, befinden.
In der Abbildung unten ist ein Balken dargestellt, der sich aus drei rechteckigen Teilkörpern zusammensetzt (wie man in der Darstellung des Querschnitts sehen kann).

Zusammengesetzter Körper mit gemeinsamer Schwerachse für alle Einzelkörper
 

Berechnung des Trägheitsmoment bei gemeinsamer Schwerachse

Dann lautet die Formel zur Berechnung des Trägheitsmoments folgendermaßen:

Das heißt im Klartext: Sofern sich die Trägheitsmomente auf die gleiche Schwerachse beziehen, dürfen sie einfach addiert werden.

Berechnung des Widerstandsmoments bei gemeinsamer Schwerachse

Die vorherige Regel gilt für Widerstands- und Biegewiderstandsmomente leider nicht. Hier muss zur Berechnung folgende Gleichung herangezogen werden (hier für die maximalen Abstände von der Schwerachse o und u):

Berechnung von Trägheitsmoment & Widerstandsmoment bei nicht zusammenfallenden Schwerachsen

Wie sieht es jedoch mit der Ermittlung des Trägheitsmomentes aus, wenn die Einzelschwerpunkte nicht auf einer gemeinsamen Schwerachse liegen?

Für die Berechnung zeichnen wir das gemeinsame Schwerachsensystem so, dass die Koordinaten y und z das gemeinsame Achsensystem des Gesamtkörpers kennzeichnen. Die Koordinaten ξ und η kennzeichnen das Schwerachsensystem des jeweiligen Einzelkörpers (siehe Abbildung unten).
Wir gehen in diesem Beispiel davon aus, dass das Trägheitsmoment des einzelnen Körpers bezüglich seiner eigenen Schwerachse bekannt ist (I_ξξ). Des Weiteren gehen wir davon aus, dass die Schwerachse des Gesamtkörpers bekannt ist (ansonsten müsste man zunächst den gemeinsamen Schwerpunkt des Gesamtkörpers berechnen).

Zusammengesetzter Körper ohne eine gemeinsame Schwerachse der Einzelkörper
 

Trägheitsmoment zusammengesetzter Querschnitte berechnen

Wie aus der Abbildung ersichtlich, gehen die Koordinaten ξ und η durch Parallelverschiebung aus den Koordinaten y und z hervor. Das Ergebnis ist der Betrag I_ξξ des Teilkörpers in Bezug zum Gesamt-Trägheitsmoment. Die zur Berechnung notwendige Formel lautet:

I_yy – Trägheitsmoment des Teilkörpers auf die Hauptachse y bezogen
I_ξξ – Trägheitsmoment des Teilkörpers auf seine eigne Schwerachse bezogen
a – Biegeachsabstand
A – Fläche des Teilkörpers

Dabei bezeichnet A die als bekannt vorausgesetzte Querschnittsfläche des betreffenden Teilkörpers. So wie in der Abbildung dargestellt entspricht der Biegeachsabstand a dem Abstand zwischen dem Flächenschwerpunkts des Teilkörpers und der y-Achse des Haupt-Koordinatensystems. Es handelt sich hierbei um den sogenannten "Satz von Steiner", welcher nun noch formal zu beweisen wäre.

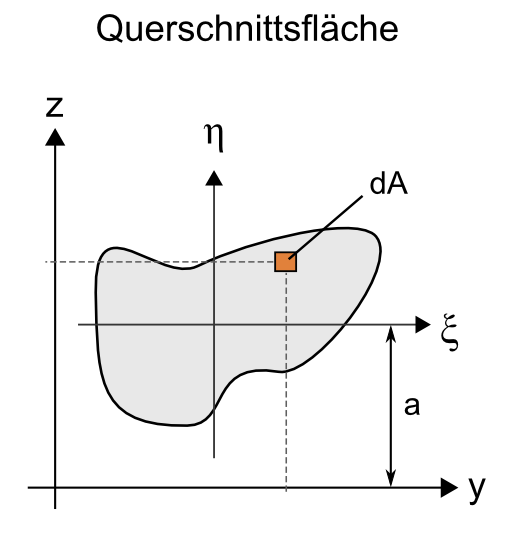Querschnittsfläche mit ξ-η-Koordinatensystem im Schwerpunkt
 

Laut Definition der teilekörpereigenen Schwerpunkte entfällt nun auch das letzte Integral und es ergibt sich folgende Gleichung:

Erkenntnis:
Das Eigenträgheitsmoment I_ξξ ist immer kleiner, als das Trägheitsmoment I_yy, welches auf eine beliebige parallele Schwerachse bezogen ist.
Die Schwierigkeit bei der Anwendung des "Satzes von Steiner" besteht allerdings zumeist darin, den Abstand a zu ermitteln. In der Praxis bedient man sich hierzu einer speziellen Tabellenkalkulation. Ein Beispiel findet Ihr in diesem Skript:
Aufgabe – Das Flächenträgheitsmoment von zusammengesetzten Körpern berechnen

Widerstandsmoment eines beliebigen Querschnitts berechnen

Das Widerstandsmoment berechnet sich auch hier wie gewohnt. Man muss dabei nur darauf achten, dass man den Abstand immer von der Haupt-Schwerachse misst.

W_y – Widerstandsmoment
I_yy – Flächenträgheitsmoment des gesamten Körpers
z – Abstand zur Schwerachse

Die schwierigere Aufgabe ist hier also mal wieder, das Flächenträgheitsmoment zu ermitteln.