Bereits in den vorhergehenden Skripten wurden verschiedene Statik-Aufgaben zum Thema Schnitt, Freischneiden und Schnittreaktionen gezeigt, in denen unterschiedliche Lastfälle vorlagen. In dieser Aufgabe liegt ein abgewinkelter Balken vor.

Aufgabe 4 - Schnittreaktionen in einem abgewinkelten Balken

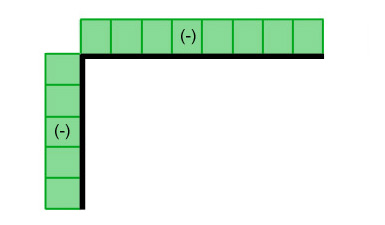
Wie bereits erwähnt liegt in diesem Beispiel ein abgewinkelter Stab vor, der durch die Kräfte F₁ und F₂ belastet wird. Durch die Tatsache, dass der Balken abgewinkelt ist, ergeben sich einige Besonderheiten. Gesucht sind in dieser Aufgabe die Schnittreaktionen in Bereich I, II und III sowie die Kraft- und Biegemoment-Verlauf der Schnittreaktionen.

Gegeben:

F₁ = 1500N
F₂ = 800N
a = 4m
b = 3m

Gesucht:

Auflagerkräfte: F_A, F_By, F_Bx
Schnittkräfte: N, Q, M_b

Statisches System – abgeknickter Balken

Lösung der Aufgabe:

Zur Lösung unseres Beispiels ist als erstes festzustellen, das das System statisch bestimmt ist. Das bedeutet, dass die Aufgabe eindeutig gelöst werden kann.
Bestimmen wir zuerst die Auflagerkräfte F_A, F_By und F_Bx. Dabei ist F_Bx am leichtesten zu bestimmen, da dieser Lagerreaktion nur die Kraft F₂ gegenübersteht. Somit stellen wir als erstes das Kräftegleichgewicht in x-Richtung auf.

∑F_x = 0 = F₂ – F_Bx
F_Bx = F₂ = 800N

Die Berechnung der Lagerkräfte F_A und F_By erfolgt über das Kräftegleichgewicht in y-Richtung und das Momentengleichgewicht um den Punkt A.

∑M_A = 0 = F_By*a + F_Bx*a - F₁*b
F_By = (F₁*b – F_Bx*a) / a = (1500N*3m – 800N*4m) / 4m = 325N

∑F_y = 0 = F₁ - F_A - F_By
F_A = F₁ – F_By = 1500N - 325N = 1175N

Nun geht es in der Aufgabe weiter mit der Berechnung der Schnittkräfte. Da auch die Kraft- und Momentenverläufe über den Balken dargestellt werden sollen, müssen die Schnittkräfte an mehreren Stellen bestimmt werden. Die drei Schnitte sind im Bild oben bereits eingezeichnet.

Beginnen wir mit dem Schnitt in Bereich I:

Bereich I - links:

N(x) = -F₂ = -800N

Q(x) = -F₁ - (-F_A) = -1500N + 1175N = -325N

M_b(x) = -(F_A*x - F₁*(x-b) - F₂*a)
M_b(x=b) = -F_A*b + F₂*a = -1175N * 3m + 800N * 4m = -325Nm
M_b(x=a) = -F_A*a + F₁*(a-b) + F₂*a = -1175N*4m + 1500N*1m + 800N*4m = 0Nm

Bereich II - links:

 N(x) = -F₂ = -800N

Q(x) = -(-F_A) = 1175N

M_b(x) = -(F_A*x - F₂*a)
M_b(x=0) = F₂*a = 800N * 4m = 3200Nm
M_b(x=b) = -(F_A*b - F₂*a) = -1175N*3m + 800N*4m = -325Nm

Anmerkung: Das die Berechnung des Biegemoments für Bereich II an der Stelle x=b das gleiche Ergebnis hervorbringt wie die Berechnung für Bereich I ist logisch, da in beiden Fällen die gleiche Stelle berechnet wurde.

Bereich III

Der Schnitt in Bereich III geht durch den Balken der senkrecht zur x-Achse steht. Wenn wir hier Freischneiden müssen wir die Vorzeichenregelung für die Schnittkräfte beachten. Es gelten folgenden allgemein gültigen Vorzeichen-Regeln für das Kräftegleichgewicht in y-Richtung und das Momentengleichgewicht.

Die Summe aller Normalkräfte und aller äußeren Kräfte in y-Richtung ist gleich 0.

=> oben: N(y) = - ∑F_y
=> unten: N(y) = + ∑F_y

Die Summe aller Querkräfte und aller äußeren Kräfte in y-Richtung ist gleich 0.

=> oben: Q(y) = - ∑F_y
=> unten: Q (y) = + ∑F_y

Die Summe aller Biegemomente und aller äußeren Momente ist gleich 0.

=> oben: M_b(y) = - ∑M
=> unten: M_b(y) = + ∑M

Mit Hilfe dieser Vorzeichen-Regeln können wir nun mit der Berechnung der Schnittkräfte in Bereich III beginnen.

Bereich III - oben:

N(y) = -F₁ - (-F_By) = -1500N + 325N = -1175N

Q(y) = -(-F_Bx) = 800N

M_b(y) = -(F_Bx*y + F_By*a - F₁*b) = F₁*b – F_Bx*y – F_By*a
M_b(y=0) = F₁*b – F_By*a = 1500N*3m – 325N*4m = 3200Nm
M_b(y=a) = F₁*b – F_Bx*a – F_By*a = 1500N*3m – 800N*4m – 325N*4m = 0Nm

Die Berechnung für ’Bereich III unten muss die selben Werte ergeben, daher wird dieses Berechnung im Lösungsweg der Aufgabe nicht durchgeführt.

Darstellung des Kraft- und Biegemomentenverlaufs

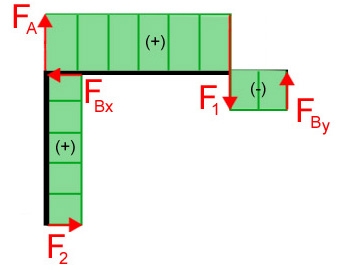
Nachdem mit Hilfe des Freischneidens alle Inneren Kräfte ermittelt wurden, kann man nun die Kraftverläufe und den Biegemomentenverlauf zeichnen. Die Kräfte werden über den Balken so eingezeichnet wie sie berechnet wurden.

Normalkraft-Verlauf

Querkraft-Verlauf

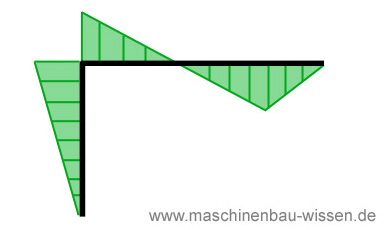
Der Sprung von einer Querkraft mit positivem Vorzeichen zu einer (kleineren) Querkraft mit negativem Vorzeichen erfolgt an der Stelle x=b. Der Bereich 0≤x≤b war der Bereich II, für den wir eine Querkraft von 1175N berechnet hatten. Im Bereicht I b≤x≤a berechneten wir eine Querkraft von -325N.

Biegemomenten-Verlauf

In der folgenden Aufgabe* soll ein letzter Sonderfall betrachtet werden: Ein Balkensystem. Diese Statik-Aufgabe finden Sie wie immer in der Hauptübersicht des Statik-Skripts.