In diesem Artikel des Kinetik-Skripts geht es um das Trägheitsmoment. Das Trägheitsmoment ist ein Begriff aus dem Bereich der Physik bzw. Kinetik. Hier erfahren Sie, wie man das Trägheitsmoment berechnen kann und was man genau unter dem Begriff versteht.

Definition - Trägheitsmoment

Das Trägheitsmoment, auch Inertialmoment oder Massenträgheitsmoment genannt, ist eine Größe der klassischen Physik, die erstmals im Jahre 1740 von Leonhard Euler beschrieben wurde. Vor allem in der Mechanik wird sie häufig verwendet. Das Massenträgheitsmoment definiert genau den Widerstand, den ein starrer Körper einer Änderung seiner Rotationsbewegung entgegenbringt. In der älteren Literatur findet sich anstatt Trägheitsmoment oft auch die Bezeichnung Drehmasse.

Massenträgheitsmoment einer Punktmasse

Das Trägheitsmoment berechnen

Das Trägheitsmoment wird in der Physik zumeist mit dem Symbol J gekennzeichnet. Für einen einzigen definierten Massenpunkt lässt sich das Massenträgheitsmoment mithilfe folgender Formel recht einfach berechnen:

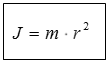
m – Masse [kg]
r – Abstände von der Drehachse [m]

Der Abstand des Massenpunktes hängt dabei von der Rotationsachse des Körpers ab. Je weiter der betrachtete Massenpunkt von der Rotationsachse entfernt ist, umso größer ist sein Massenträgheitsmoment. Das bedeutet, dass mehr Kraft erforderlich ist, um den Körper in Rotation zu versetzen.

Ein physikalischer Körper besteht jedoch nicht nur aus einem Massenpunkt, sondern aus unzählig vielen. Zur Ermittlung des gesamten Trägheitsmomentes müssen deshalb alle Massenpunkte und deren Abstände zur Drehachse betrachtet werden. Deshalb ist es in der Praxis vergleichsweise kompliziert, das Trägheitsmoment komplexer Körper exakt zu berechnen. Selbst bei einfachen Körpern stoßen Physiker und Mathematiker an Grenzen.

Das Trägheitsmoment in der Praxis

Obwohl uns das Trägheitsmoment mitsamt seinen Auswirkungen im Alltag sehr oft begegnet, wird es, wie viele andere physikalische Zusammenhänge, in aller Regel nicht bewusst wahrgenommen. Doch gerade im Sport, etwa beim Pirouettendrehen oder Saltoschlagen ist das Trägheitsmoment entscheidend. Ziel von Sportlern und Trainern ist es natürlich, das Massenträgheitsmoment so zu optimieren, dass das Ergebnis zum Sieg führt.

Eine Pirouette beispielsweise, sollte besonders schnell ablaufen. Dazu muss der Sportler versuchen, seinen Massenschwerpunkt so dicht wie möglich an seine Rotationsachse zu bekommen, indem er Arme und Beine eng an den Körper anlegt. Weil gemäß Formel der Abstand sogar quadratisch eingeht, rufen bereits kleine Veränderungen große Wirkungen hervor.

Ähnlich verhält es sich bei einem Salto. Damit sich der Athlet schnell um seine eigene Achse drehen kann, sollte der Sportler ein möglichst geringes Trägheitsmoment aufweisen. Das bedeutet, dass sich alle Körperteile so eng wie nur möglich am Körper befinden müssen und der gesamte Rumpf eingerollt ist.

Zusammenhang Trägheitsmoment und lineare Bewegung

Anhand der jeweiligen Gleichungen ist zu erkennen, dass sich das Massenträgheitsmoment bei Rotation durchaus mit der Masse einer geradlinigen Bewegung vergleichen lässt.

Rotationsbewegung: Das Drehmoment errechnet sich aus dem Trägheitsmoment mal Winkelbeschleunigung.

Geradlinige Bewegung: Die Kraft errechnet sich aus der Masse mal Beschleunigung. Diese Definition entspricht dem Zweiten Newtonschen Gesetz.

Allgemeine Definition – Berechnung des Trägheitsmoments

Bei bekannter Massenverteilung ρ(r) eines Körpers lässt sich das Massenträgheitsmoment J aus folgendem Volumenintegral berechnen:

Dabei ist r_﬩ der zur Rotationsachse ω (Winkelgeschwindigkeit) senkrechte Anteil von r.

Zwei weitere Formeln, mit denen man das Trägheitsmoment berechnen kann, sehen wie folgt aus:

Man kann mehrere Trägheitsmoment, die sich auf die selbe Drehachse beziehen also addieren.

Oder in integraler Form:

m_i, dm – Masselemente [kg]
r_i, r – Abstände von der Drehachse [m]

Es gilt bei der Berechnung des Massenträgheitsmomentes zu beachten, dass das Trägheitsmoment eines beliebigen Körpers von seiner Masse und der Masseverteilung bezogen auf die Drehachse abhängig ist. Am einfachsten ist das Trägheitsmoment zu berechnen, wenn die Drehachse durch den Schwerpunkte (Massemittelpunkt) verläuft. Diesen Sonderfall sehen wir uns im nachfolgenden Tutorial an.

Flächenträgheitsmoment

Eine verwandte physikalische Größe aus dem Bereich der Mechanik stellt das Flächenträgheitsmoment dar. Es sollte jedoch auf keinen Fall mit der (Massen-)Trägheitsmoment verwechselt werden. Mehr zu diesem Thema lesen Sie im entsprechenden Artikel: Flächenträgheitsmoment