In der Technischen Mechanik* ist die Steifigkeit eine Größe, mittels der beschrieben wird, welchen Widerstand ein Körper gegen eine Verformung durch äußere Einwirkung (Drehmoment oder Kraft) leisten kann. In der Folge ist die Steifigkeit von zwei Faktoren abhängig: Von der Geometrie des Körpers sowie von dessen Werkstoff. Man unterscheidet dabei generell zwischen unterschiedlichen Steifigkeiten wie beispielsweise Dehn-, Torsions- und Biegesteifigkeit. Die Unterscheidung ist abhängig von der Belastungsart. Der Kehrwert der Steifigkeit ist die Nachgiebigkeit.

Arten der Steifigkeit in der Mechanik

Steifigkeiten bestehen aus zwei Größenwerten: Einem Geometrie- sowie einem Werkstoffterm. Die Frage, welche Größe für den Werkstoff (Elastizitäts- oder Schubmodul) zur Verwendung kommt, ist von der Beanspruchung abhängig. Diese wird ihrerseits von der Belastung erzeugt. Man notiert Steifigkeiten dabei auf eine Weise, dass die Verformungsgrößen kenntlich werden - z.B. Dehnungen und keine Längenänderungen. Der Hintergrund ist simpel: Die Steifigkeit gehört zum Querschnitt des Objekts. Die Querschnittsgeometrie kann sich über die Gesamtlänge (wie z.B. bei einer Flasche) ändern, sodass eine Multiplikation mit der Länge zu Fehlern führen würde.

Die Dehnsteifigkeit

Als Produkt des Elastizitätsmoduls E (Werkstoff in Belastungsrichtung) und der Querschnittsfläche A (Senkrecht zur Belastungsrichtung) entsteht die Dehnsteifigkeit in der Mechanik. Ihre Formel lautet folglich:

Diese Formel bezieht sich dabei allerdings auf eine freie Querkontraktion vom Querschnitt. Ist die Querkontraktion jedoch eingeschränkt, muss das querkontraktionsbehinderte Modul verwendet werden. Dafür wird der Elastizitätsmodul ausgelassen.

Die Längsdehnung des Körpers wird mit dem Buchstaben ε kenntlich gemacht. Sie ist umgekehrt proportional zur Dehnsteifigkeit und Normalproportional zu der sie angreifenden Normalkraft, die mit dem Buchstaben F beschrieben wird. Es folgt daraus folgende Formel:
    

Die Biegesteifigkeit

Das Produkt aus dem Flächenträgheitsmoment I sowie dem Elastizitätsmodul E ist die sogenannte Biegesteifigkeit. Zu beachten ist dabei, dass das Flächenträgheitsmoment wesentlich von der Querschnittsform abhängig ist. Es folgt:

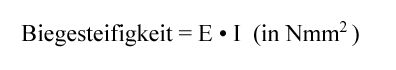
Neben der Biegesteifigkeit sind auch die Lagerungsbedingungen sowie die Länge eines Bauteils, das gebogen wird, dafür maßgeblich, wie kräftig seine Durchbiegung erfolgen kann. Die Durchbiegung wird als Krümmung κ bezeichnet. κ ist proportional zum angreifenden Biegemoment M_B. Die Krümmung verhält sich außerdem umgekehrt proportional zur Biegesteifigkeit.

Die Torsionssteifigkeit

Die Torsionssteifigkeit wird gelegentlich auch als Verwindungssteifigkeit beschrieben. Sie ist das Ergebnis aus dem Produkt des zugehörigen Torsionsträgheitsmoment I_T sowie dem Werkstoffschubmoduls G. I_T ist dabei auf die Achse zu beziehen, um die das Bauteil tordiert wird.

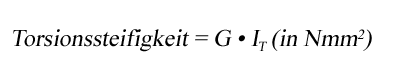
Zu beachten ist, dass I_T nicht generell dem polaren Querschnittsflächenträgheitsmoment Ip entspricht. Dies ist nur bei Kreisquerschnitten sowie bei Kreisringquerschnitten der Fall. Für I_T lässt sich nur bei Spezialfällen eine geschlossene Formel nennen.

Für die Frage, wie stark sich ein Bauteil unter einer Belastung verdreht, hängt neben I_T auch von der Länge L sowie von den Bedingungen der Lagerung ab. Man bezeichnet dabei die Verdrehung pro L-Einheit als Verwindung oder Drillung (ʋ'). Die Verwindung ist proportional zum Torsionsmoment M_T und umgekehrt proportional zur Torsionssteifigkeit. Es folgt:

Steifigkeit und Festigkeit

Zu beachten ist zudem, dass Steifigkeit nicht mit Festigkeit* verwechselt werden darf. Die Festigkeit ist ein Maß dafür, wie groß die ertragbare Belastung eines Werkstoffs ist. Es handelt sich folglich um einen Grenzwert, den man leicht in Datenblättern recherchieren kann. Ein Beispiel für die Festigkeit ist die Zugfestigkeit.

Die Steifigkeit ist hingegen von der Elastizität des Werkstoffs sowie der Form und Größe der Querschnittsfläche abhängig. Die Steifigkeit steht folglich in keinerlei Abhängigkeit zur Festigkeit.

=> Steifigkeit ≠ Festigkeit