Dieses Mechanik-Skript soll die Berechnung der Schubspannung im einachsigen Spannungszustand verständlich machen. Um das Auftreten von Schubspannungen im einachsigen Spannungszustand zu verstehen, betrachtet man am besten ein einfaches Beispiel:
Hier soll uns ein einfacher Stab dienen, dessen linkes Ende fest gelagert ist, während das rechte Ende mit einer Zugkraft beaufschlagt wird. Die Kraft und auch die Querschnittsfläche sind bekannt, womit man die Zugspannung wie gewohnt berechnen kann.

Wie man die Schubspannung im einachsigen Spannungszustand berechnen kann, werden wir hier rein theoretisch betrachtet, womit gemeint ist, dass wir keine konkreten Werte einsetzen werden.
Schnitt durch den Zugstab
Wir führen einen Schnitt durch den Zugstab aus und legen damit die wirkenden Kräfte und entstehenden Spannungen im Inneren offen. Das Freischneiden funktioniert hier genauso wie in der Statik.

Das im Inneren des Stabe eine Zugspannung entsteh, ist offensichtlich und auch leicht verständlich. Überraschender ist vielleicht die Tatsache, dass auch Schubspannungen entstehen.
Diese Schubspannungen sind unter anderem wichtig in Hinblick auf das Versagen von Werkstoffen* mit sprödem und duktilem Verhalten.
Berechnung der Schubspannung unter Zugbelastung
Um das Vorhandensein der Schubspannung in diesem einachsigen Spannungszustand zu verstehen, macht man einen Schnitt im Winkel α durch den Stab.
Betrachten wir den Stab mit diesem Schnitt erneut:
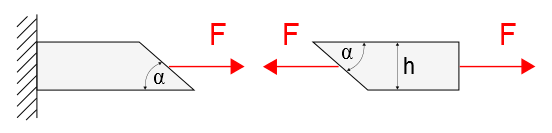
Auch unter diesem Schnitt muss das Kräftegleichgewicht vorhanden sein (wie wir es in der Statik gelernt haben). Man beachte bei diesem Schnitt jedoch, dass die Kraft F auf eine schräge Fläche wirkt. Dies ist bei der Berechnung der Spannungen von Bedeutung.
Diese schräge Fläche A’ ist größer als die normale Querschnittsfläche A des Stabes. Da sich die Spannung aus der Division „Kraft : Fläche“ ergibt, muss die Spannung in dieser Fläche A’ geringer sein als die Zugspannung in der Querschnittsfläche A. Diese Erkenntnis ist jedoch noch zweitrangig – wichtig ist, dass hier eine andere Spannung vorliegt, als beim Schnitt senkrecht durch den Stab. Wir nennen dies Spannung t(α). Sie berechnet sich wie folgt:
Bereits in der Statik wurde gezeigt, dass man Kräfte mit Hilfe des Kräfteparallelogramms* zerlegen kann. Dies gelingt auch mit Spannungen.
Wir können also die Spannung t(α) in zwei Spannungen mit unterschiedlicher Richtung zerlegen:
a) eine Spannung σ normal zu Schnittfläche (= 90° zur Schnittfläche) und
b) eine Spannung τ parallel zur Schnittfläche (das ist die Schubspannung).

Die Berechnung dieser beiden Spannungen ist mit dem Sinus- bzw. Cosinus-Satz relativ einfach
Zum Verständnis
Machen Sie sich an dieser Stelle Gedanken darüber, was mit den beiden Spannungen passiert, wenn man den Winkel des Schnittes verändert.
Unter welchem Schnittwinkel ist welche Spannung am höchsten bzw. geringsten?
Denken Sie hier daran, wie sich die Fläche A’ verändert, was das für die Spannung t(α) (= F/A’) bedeutet und wie sich dies wiederum auf die beiden Spannungen σ und τ auswirkt.
Maximale Normalspannung
Bei richtiger Überlegung wird klar, dass die maximale Normalspannung σ unter einem Schnittwinkel von 90° auftritt. Grund ist, dass hier die Schnittfläche A am geringsten ist, somit entsteht die größte mechanische Spannung* (die Kraft ist auf eine geringe Fläche verteilt).
Die Schubspannung τ ist unter diesem Winkel gleich 0.
 Schubspannung und Normalspannung im 90°-Schnitt
Schubspannung und Normalspannung im 90°-Schnitt
Spannungen im 0°-Schnitt
Im 0°-Schnitt ist das Stab in der gesamten Länge geschnitten. Die Schnittfläche wird hier extrem groß. Sowohl Normalspannung, als auch Schubspannung sind entsprechend = 0.

Spannung im 0°-Schnitt
Maximale Schubspannung
Unter welchem Schnittwinkel die maximale Schubspannung auftritt, lässt sich auf dem rechnerischen Weg ermitteln (das ist etwas komplizierter als die beiden vorhergehenden Fälle). Die Berechnung gelingt durch die Ableitung von τ nach α:
Die Berechnung ergibt also, dass die höchsten Schubspannungen im einachsigen Spannungszustand unter einem Winkel von 45° auftreten. Der Wert der maximalen Schubspannung ergibt sich durch das Einsetzen des Winkels α =45° in unsere zuvor hergeleitete Formel.
Bedeutung für das Materialversagen unter Zuglast
Das Auftreten der maximalen Spannungen unter den Winkeln von 0° und 45° hat weitreichende Folgen für das Materialverhalten verschiedener Werkstoffe*.
a) Für spröde Werkstoffe ist die maximale Normalspannung ausschlaggebend. Hier tritt ein Trennbruch bzw. Spaltbruch unter einem Winkel von 0° auf.
b) Für duktile (zähe) Werkstoffe ist die Schubspannung unter Zugbeanspruchung entscheidend. Zähe Werkstoffe versagen hier häufig in Form eines Gleitbruchs bzw. Scherbruchs, der im Winkel von 45° auftritt.
Weitere Bedeutung der Erkenntnisse aus dieser Betrachtung
Die Erkenntnisse, aus der hier durchgeführten Betrachtung, sind auch für das Verständnis des Mohr’schen Spannungskreises sehr hilfreich. Hierzu kommen wir in einem späteren Kapitel der Technischen Mechanik*.
Die Normalspannung und Schubspannung im einachsigen Spannungszustand lassen sich im Mohr’schen Spannungskreis sehr gut darstellen und sind hier ein noch relativ einfaches Beispiel, das entsprechend oft herangezogen wird.



